There are many radiometric clocks and when applied to appropriate materials, the dating can be very accurate. As one example, the first minerals to crystallize condense from the hot cloud of gasses that surrounded the Sun as it first became a star have been dated to plus or minus 2 million years!! That is pretty accurate!!! Other events on earth can be dated equally well given the right minerals. For example, a problem I have worked on involving the eruption of a volcano at what is now Naples, Italy, occurred years ago with a plus or minus of years.
Yes, radiometric dating is a very accurate way to date the Earth. We know it is accurate because radiometric dating is based on the radioactive decay of unstable isotopes. For example, the element Uranium exists as one of several isotopes, some of which are unstable. When an unstable Uranium U isotope decays, it turns into an isotope of the element Lead Pb.
We call the original, unstable isotope Uranium the "parent", and the product of decay Lead the "daughter".
From careful physics and chemistry experiments, we know that parents turn into daughters at a very consistent, predictable rate. A geologist can pick up a rock from a mountainside somewhere, and bring it back to the lab, and separate out the individual minerals that compose the rock. They can then look at a single mineral, and using an instrument called a mass spectrometer, they can measure the amount of parent and the amount of daughter in that mineral.
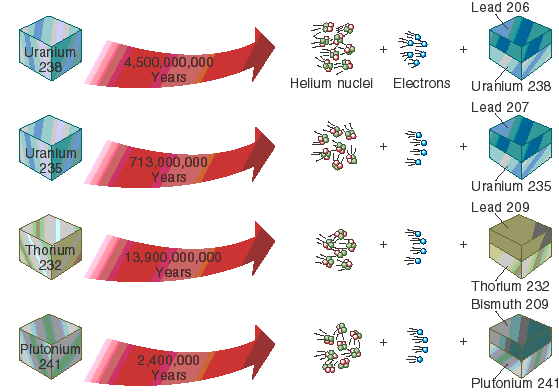
The ratio of the parent to daughter then can be used to back-calculate the age of that rock. The reason we know that radiometric dating works so well is because we can use several different isotope systems for example, Uranium-Lead, Lutetium-Halfnium, Potassium-Argon on the same rock, and they all come up with the same age. This gives geologists great confidence that the method correctly determines when that rock formed.
Hope that helps, and please ask if you'd like more details! I think that I will start by answering the second part of your question, just because I think that will make the answer to the first question clearer. Radiometric dating is the use of radioactive and radiogenic those formed from the decay of radioactive parents isotopes isotopes are atoms of the same element that have different numbers of neutrons in their nuclei to determine the age of something.
It is commonly used in earth science to determine the age of rock formations or features or to figure out how fast geologic processes take place for example, how fast marine terraces on Santa Cruz island are being uplifted. Radiometric dating relies on the principle of radioactive decay.
Explain how radiometric dating is used to estimate absolute age
All radioactive isotopes have a characteristic half-life the amount of time that it takes for one half of the original number of atoms of that isotope to decay. By measuring the parent isotope radioactive and the daughter isotope radiogenic in a system for example, a rock , we can tell how long the system has been closed in our example, when the rock formed. The process of radiogenic dating is usually done using some sort of mass spectrometer. A mass spectrometer is an instrument that separates atoms based on their mass.
Radiometric Dating: Methods, Uses & the Significance of Half-Life
Because geochronologists want to measure isotopes with different masses, a mass spectrometer works really well for dating things. I do think that radiometric dating is an accurate way to date the earth, although I am a geochronologist so I have my biases. Most estimates of the age of the earth come from dating meteorites that have fallen to Earth because we think that they formed in our solar nebula very close to the time that the earth formed. The fact that the age we calculate is reproducible for these different systems is significant. We have also obtained a very similar age by measuring Pb isotopes in materials from earth.
I should mention that the decay constants basically a value that indicates how fast a certain radioactive isotope will decay for some of these isotope systems were calculated by assuming that the age of the earth is 4. The decay constants for most of these systems have been confirmed in other ways, adding strength to our argument for the age of the earth. Radiometric dating depends on the chemistry and ratios of different elements. It works like this:. Take, for example, zircon, which is a mineral; its chemical formula is ZiSiO 4 , so there is one zirconium Zi for one silicon Si for four oxygen O.
Navigation menu
One of the elements that can stand in chemically for zircon is uranium. Uranium eventually decays into lead, and lead does not normally occur in zircon, except as the radioactive decay product of uranium. This transformation may be accomplished in a number of different ways, including alpha decay emission of alpha particles and beta decay electron emission, positron emission, or electron capture.
Another possibility is spontaneous fission into two or more nuclides. While the moment in time at which a particular nucleus decays is unpredictable, a collection of atoms of a radioactive nuclide decays exponentially at a rate described by a parameter known as the half-life , usually given in units of years when discussing dating techniques. After one half-life has elapsed, one half of the atoms of the nuclide in question will have decayed into a "daughter" nuclide or decay product. In many cases, the daughter nuclide itself is radioactive, resulting in a decay chain , eventually ending with the formation of a stable nonradioactive daughter nuclide; each step in such a chain is characterized by a distinct half-life.
In these cases, usually the half-life of interest in radiometric dating is the longest one in the chain, which is the rate-limiting factor in the ultimate transformation of the radioactive nuclide into its stable daughter. Isotopic systems that have been exploited for radiometric dating have half-lives ranging from only about 10 years e. For most radioactive nuclides, the half-life depends solely on nuclear properties and is essentially a constant. It is not affected by external factors such as temperature , pressure , chemical environment, or presence of a magnetic or electric field.
For all other nuclides, the proportion of the original nuclide to its decay products changes in a predictable way as the original nuclide decays over time. This predictability allows the relative abundances of related nuclides to be used as a clock to measure the time from the incorporation of the original nuclides into a material to the present.
The basic equation of radiometric dating requires that neither the parent nuclide nor the daughter product can enter or leave the material after its formation. The possible confounding effects of contamination of parent and daughter isotopes have to be considered, as do the effects of any loss or gain of such isotopes since the sample was created. It is therefore essential to have as much information as possible about the material being dated and to check for possible signs of alteration.
Alternatively, if several different minerals can be dated from the same sample and are assumed to be formed by the same event and were in equilibrium with the reservoir when they formed, they should form an isochron. This can reduce the problem of contamination. In uranium—lead dating , the concordia diagram is used which also decreases the problem of nuclide loss. Finally, correlation between different isotopic dating methods may be required to confirm the age of a sample.
For example, the age of the Amitsoq gneisses from western Greenland was determined to be 3. Accurate radiometric dating generally requires that the parent has a long enough half-life that it will be present in significant amounts at the time of measurement except as described below under "Dating with short-lived extinct radionuclides" , the half-life of the parent is accurately known, and enough of the daughter product is produced to be accurately measured and distinguished from the initial amount of the daughter present in the material.
The procedures used to isolate and analyze the parent and daughter nuclides must be precise and accurate.
Radiometric dating
This normally involves isotope-ratio mass spectrometry. The precision of a dating method depends in part on the half-life of the radioactive isotope involved. For instance, carbon has a half-life of 5, years. After an organism has been dead for 60, years, so little carbon is left that accurate dating cannot be established. On the other hand, the concentration of carbon falls off so steeply that the age of relatively young remains can be determined precisely to within a few decades.
If a material that selectively rejects the daughter nuclide is heated, any daughter nuclides that have been accumulated over time will be lost through diffusion , setting the isotopic "clock" to zero. The temperature at which this happens is known as the closure temperature or blocking temperature and is specific to a particular material and isotopic system.
These temperatures are experimentally determined in the lab by artificially resetting sample minerals using a high-temperature furnace.
As the mineral cools, the crystal structure begins to form and diffusion of isotopes is less easy. At a certain temperature, the crystal structure has formed sufficiently to prevent diffusion of isotopes. This temperature is what is known as closure temperature and represents the temperature below which the mineral is a closed system to isotopes.
Thus an igneous or metamorphic rock or melt, which is slowly cooling, does not begin to exhibit measurable radioactive decay until it cools below the closure temperature.
Explainer: what is radiocarbon dating and how does it work?
The age that can be calculated by radiometric dating is thus the time at which the rock or mineral cooled to closure temperature. This field is known as thermochronology or thermochronometry.
- .
- early dating love quotes!
- long beach ca dating!
- Dating history!
- lonely dating sites!
- campus dating sites in kenya!
The mathematical expression that relates radioactive decay to geologic time is [12] [15]. The equation is most conveniently expressed in terms of the measured quantity N t rather than the constant initial value N o. The above equation makes use of information on the composition of parent and daughter isotopes at the time the material being tested cooled below its closure temperature.
